Геометрия без ограничений | Создание ячеистых и сетчатых структур | Сокращение числа единиц в сборке
Если говорить сухим академическим языком, топологическая оптимизация – это процесс изменения конструкции, структуры детали и ее варьирующихся параметров при заданном критерии оптимальности с сохранением или улучшением ее функционала.
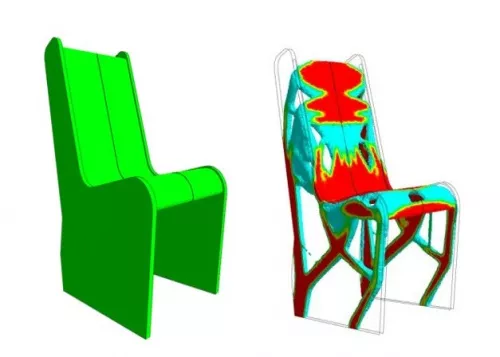
Возьмем две детали, выполняющие одну и ту же функцию с определенными нагрузками и имеющие определенный ресурс. По сути, это одна и та же деталь, но с разной геометрией. Геометрия первой детали оптимизирована для изготовления стандартными методами производства: на фрезерном, токарном станке и средствами других технологий металлообработки. Это простая и плоская геометрия, ее легко добиться при обработке на станке. У второй детали геометрия более сложная, и сделать ее на станке представляет серьезные трудности.
Геометрия без ограничений
Когда еще не существовало аддитивных технологий, а были только субтрактивные, то вопрос геометрии не стоял так остро и решался доступными способами. Топологическая оптимизация позволяет изменить стандартную геометрию на геометрию, специально адаптированную под определенную технологию. И это может быть и традиционная технология (например, литье), и аддитивный процесс.
Согласно данным, у второй детали меньше напряжение, меньше перемещение под нагрузкой и, самое главное, вес уменьшился на 1 кг. Для одной детали немного, но если их выпускают сто тысяч в год, то суммарно мы можем сэкономить сто тонн металла только на одной детали.
Эксперты iQB Technologies рекомендуют статью Российский производитель SLM-машин развеивает мифы о технологии
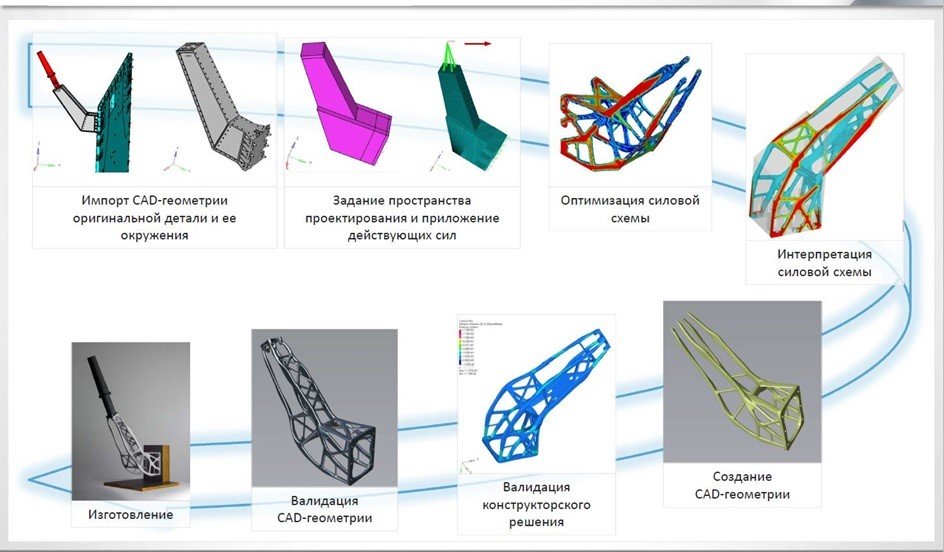
Программное обеспечение для топологической оптимизации не строит модель объекта с нуля. В него загружается геометрическая модель изделия, ранее изготовленного другим методом. На рисунке приведен пример изделия с простыми плоскими формами и заклепками, болтами, приваренными ребрами. Когда мы загрузили модель, мы отмечаем места, которые не полежат изменению. В данном случае это крепления. Все остальное, что не попало в эти зоны, но принадлежит детали, является так называемой design space, то есть той зоной, где программа может менять геометрию.
Затем мы в соответствии со служебным назначением изделия накладываем нагрузки, которые деталь должна выдерживать, то есть создаем силовую схему нагрузок. И далее, на основе заданных нами параметров, программа начинает создавать новую оптимизированную геометрию. Между двумя неизменными местами для крепления она выстраивает новую модель. Она анализирует напряжение в каждом сечении – выдерживает его сечение или нет. Если не выдерживает, то программа меняет сечение.

Оптимизированная алюминиевая и исходная стальная стойки с запрессованным подшипником и шаровой
Процесс построения новой модели довольно затратный по времени и требует больших вычислительных ресурсов. Этот метод моделирования называется методом конечных элементов. Для каждой точки изделия программа составляет и решает интегральные уравнения, учитывая при этом взаимосвязи между всеми точками. В результате расчета получается новая геометрия. Затем конструктор может изменить что-то в модели, если это необходимо. В итоге получается CAD-модель.
Далее для верификации модель загружается в другое программное обеспечение, в котором она проходит финальную проверку на максимальные деформации, напряжения и пр. Затем геометрия утверждается и может быть передана в производство. При этом программа умеет оптимизировать геометрию под разные виды производства: под литье, штамповку, ковку или под аддитивное производство.
Топологическая геометрия, как правило, имеет аморфные формы, в ней нет плоских, прямых линий, могут быть сплайны второго порядка. При соблюдении тех же самых свойств и нагрузочных характеристик такое моделирование позволяет уменьшить массу изделия, и, следовательно, сократить издержки на производство. Понижение массы изделия при сохранении функционала изделия – это задача номер один в самолетостроении, авиакосмической отрасли и автомобилестроении.
Рекомендуем программный продукт Materialise 3-matic
Создание ячеистых и сетчатых структур
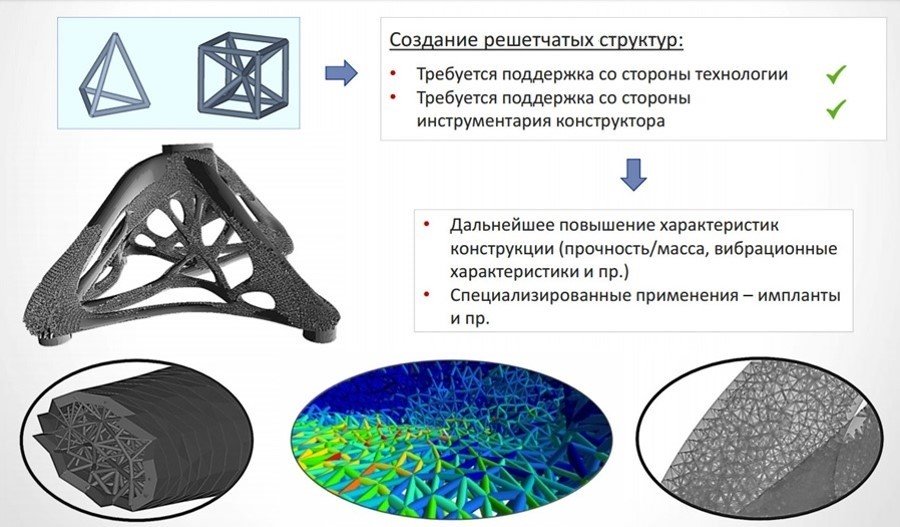
В природе такие структуры встречаются очень часто. Кости птиц могут быть почти пустотелыми, а кость млекопитающих представляет из себя жесткую оболочку с губчатой структурой внутри. Это позволяет выдерживать те же нагрузки при меньших затратах организма на выращивание такой кости и меньшем весе.
Топологическая оптимизация дает возможность делать решетчатые структуры разных форм и размеров (например, гексагоновые) или создавать ячеистую структуру, а снаружи – твердую оболочку. Стандартными методами такую структуру нельзя изготовить – только с использованием аддитивных технологий.
Сокращение числа единиц в сборке
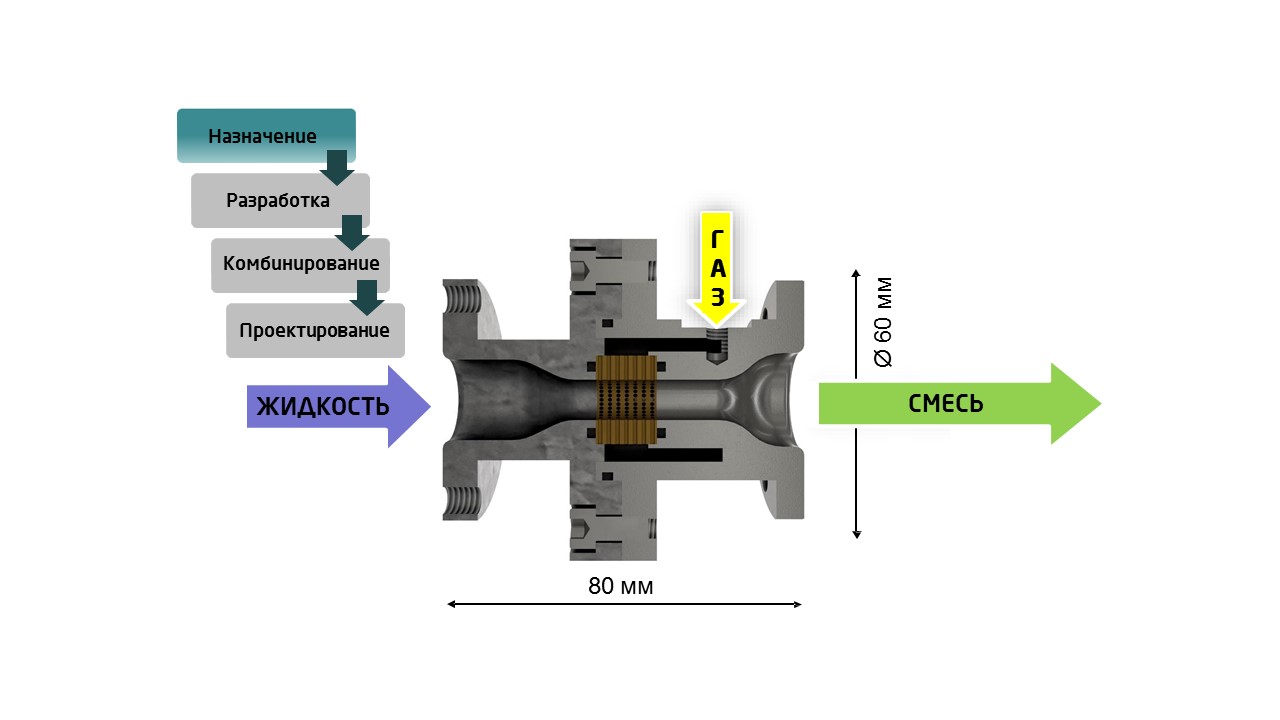
Это еще одно преимущество топологической оптимизации вместе с аддитивными технологиями. Пример: на рисунке изображен типичный сатуратор (смеситель жидкости с газом). Внутри трубы стоит маленький фильтр. Чтобы установить его туда, необходимо эту деталь сделать разъемной в двух частях, сделать фланцы для крепления, а также прокладки, болты и т.д.
С помощью аддитивных технологий можно в одном корпусе создать и саму трубу, и мелкий фильтр внутри, и канал вокруг для распределения газа.
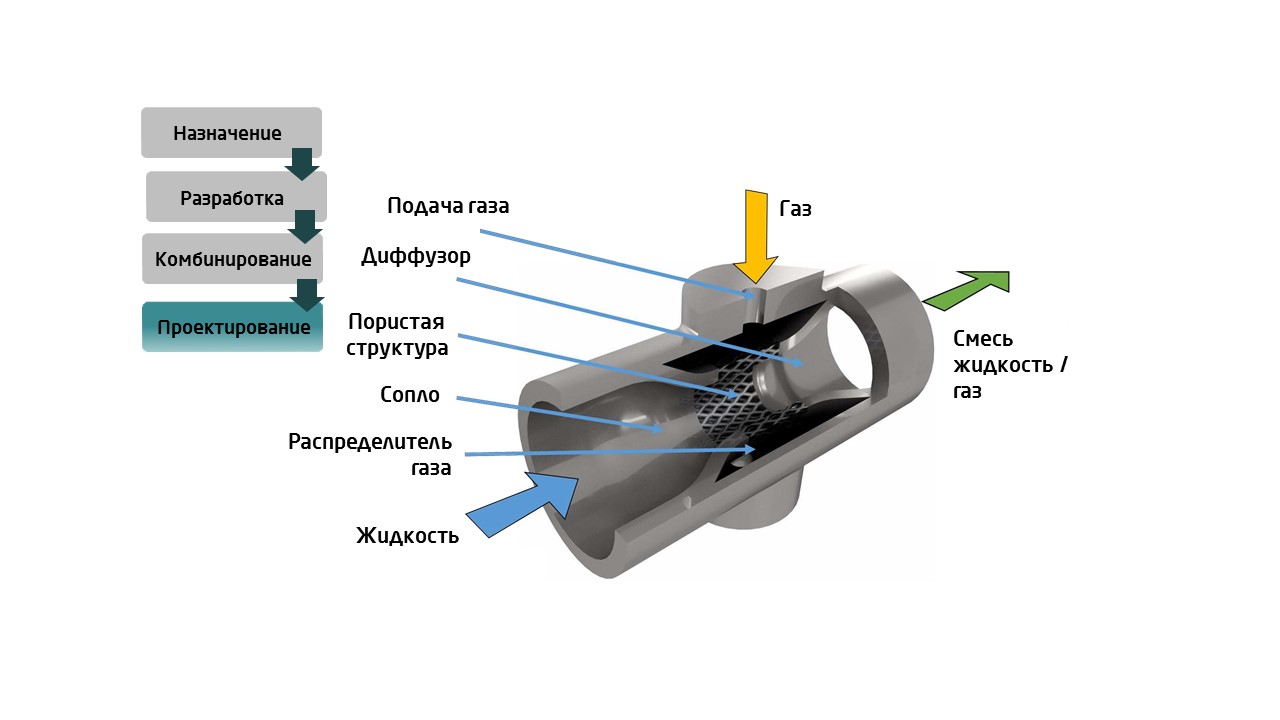
В итоге, применяя 3D-печать металлом, получаем в цельном корпусе единую деталь, одну единицу хранения. Теперь не требуется операция сборки, нет прокладок, которые могут течь, нет больших фланцев, на которые уходил металл.
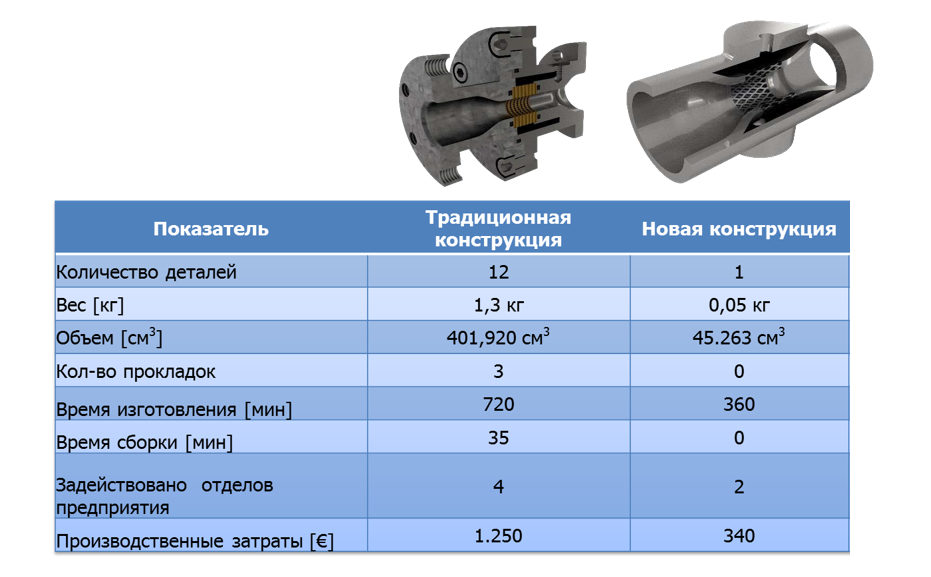
Если мы уменьшаем вес детали в самолете всего на 200 г, а в нем таких деталей 100, то мы экономим 20 кг, а при ресурсе самолета в 25 лет это огромная экономия топлива или лишняя полезная нагрузка.
Таким образом, топологическая оптимизация – это моделирование в специализированном программном обеспечении, которое позволяет создать геометрию без ограничений.
Статья опубликована 10.05.2017 , обновлена 15.06.2022